Pool Shapes
These are the most common pool shapes that we install along with the different dimensions, sq.ft. area, and gallon capacity.
True-L
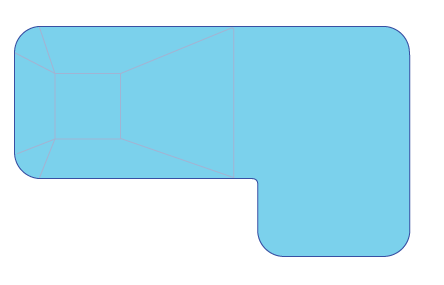
16' x 41' x 24' x 8'
Corner Radius: 6 in.
Area: 784 sq. ft.
Gallons: 33,316
Corner Radius: 2 ft.
Area: 780 sq. ft.
Gallons: 33,139
Corner Radius: 4 ft.
Area: 767 sq. ft.
Gallons: 32,586
18' x 43' x 28' x 8'
Corner Radius: 6 in.
Area: 954 sq. ft.
Gallons: 40,533
Corner Radius: 2 ft.
Area: 950 sq. ft.
Gallons: 40,363
Corner Radius: 4 ft.
Area: 937 sq. ft.
Gallons: 39,811
Rectangle
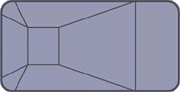
16' x 32' x 8'
Corner Radius: 6 in.
Area: 512 sq. ft.
Gallons: 21,747
Corner Radius: 2 ft.
Area: 509 sq. ft.
Gallons: 21,612
Corner Radius: 4 ft.
Area: 498 sq. ft.
Gallons: 21,173
18' x 36' x 8'
Corner Radius: 6 in.
Area: 648 sq. ft.
Gallons: 27,526
Corner Radius: 2 ft.
Area: 645 sq. ft.
Gallons: 27,392
Corner Radius: 4 ft.
Area: 634 sq. ft.
Gallons: 26,952
20' x 40' x 8'6"
Corner Radius: 6 in.
Area: 800 sq. ft.
Gallons: 35,488
Corner Radius: 2 ft.
Area: 797 sq. ft.
Gallons: 35,347
Corner Radius: 4 ft.
Area: 786 sq. ft.
Gallons: 34,889
Grecian
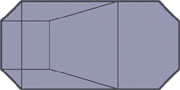
16' 6" x 32' 6" x 8'
Corner Radius: N/A
Area: 500 sq. ft.
Gallons: 21,226
18' 6" x 36' 6" x 8'
Corner Radius: N/A
Area: 639 sq. ft.
Gallons: 27,130
Lazy-L
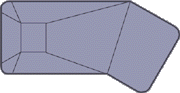
16' x 39' 3" x 8'
Corner Radius: 2 ft.
Area: 597 sq. ft.
Gallons: 25,355
16' x 38' 6" x 8'
Corner Radius: 4 ft.
Area: 588 sq. ft.
Gallons: 24,991
16' x 39' 10" x 8'
Corner Radius: 6 in.
Area: 601 sq. ft.
Gallons: 25,554
20' x 43' 4" x 8'
Corner Radius: 6 in.
Area: 809 sq. ft.
Gallons: 34,364
20' x 43' 5" x 8'
Corner Radius: 4 ft.
Area: 827 sq. ft.
Gallons: 35,133
20' x 44' x 8'
Corner Radius: 2 ft.
Area: 837 sq. ft.
Gallons: 35,568
Kidney
18' x 30' 4" x 6'
Corner Radius: N/A
Area: 441 sq. ft.
Gallons: 15,430